sistemas operativos

viernes, 18 de septiembre de 2015

función excel

Ejemplo de la función CONCATENAR

Copiar tabla en Excel para realizar el ejercicio

Nombre	Apellido	Cedula	Función
Paula Andrea	Fernández	1012340511
Johan Sebastián	Fernández	1012403324

Proceso

1. En la celda D2 comenzaré a escribir la función CONCATENAR especificando el primer argumento:

=CONCATENAR(A2,

2. Como segundo argumento debo especificar un espacio vacío de manera que el Nombre y el Apellido paternos permanezcan separados en la nueva cadena de texto:

=CONCATENAR(A2," ",

3. Ahora puedo especificar el tercer y cuarto argumento que será el Apellido paterno con su respectivo espacio:

=CONCATENAR(A2," ",B2," ",

4. Y como último paso en el quinto argumento irá el número de cedula de cada persona:

=CONCATENAR(A2," ",B2," ",C2)

domingo, 23 de agosto de 2015

La lógica proposicional o lógica de orden cero es un sistema formal cuyos elementos más simples representan proposiciones, y cuyas constantes lógicas, llamadas conectivas, representan operaciones sobre proposiciones, capaces de formar otras proposiciones de mayor complejidad.¹

La lógica proposicional trata con sistemas lógicos que carecen de cuantificadores, o variables interpretables como entidades. En lógica proposicional si bien no hay signos para variables de tipo entidad, sí existen signos para variables proposicionales (es decir, que pueden ser interpretadas como proposiciones con un valor de verdad de definido), de ahí el nombre proposicional. La lógica proposicional incluye además de variables interpretables como proposiciones simples signos para conectivas lógicas, por lo que dentro de este tipo de lógica puede analizarse la inferencia lógica de proposiciones a partir de proposiciones, pero sin tener en cuenta la estructura interna de las proposiciones más simples.

Tablas de verdad

La tabla de verdad de una fórmula es una tabla en la que se presentan todas las posibles interpretaciones de las variables proposicionales que constituye la fórmula y el valor de verdad de la fórmula completa para cada interpretación. Por ejemplo, la tabla de verdad para la fórmula

\neg (p \or q) \to (p \to r)

sería:

\begin{array}{c|c|c||c|c|c|c} p & q & r & (p \or q) & \neg (p \or q) & (p \to r) & \neg (p \or q) \to (p \to r) \\ \hline V & V & V & V & F & V & V \\ V & V & F & V & F & F & V \\ V & F & V & V & F & V & V \\ V & F & F & V & F & F & V \\ F & V & V & V & F & V & V \\ F & V & F & V & F & V & V \\ F & F & V & F & V & V & V \\ F & F & F & F & V & V & V \\ \end{array}

sistemas de numeración orientados a la informatica

En este espacio encontramos información detallada de los diferentes sistemas de numeración

sistema binario

El sistema binario, llamado también sistema diádico en ciencias de la computación, es un sistema de numeración en el que los números se representan utilizando solamente las cifras cero y uno (0 y 1). Es uno de los que se utilizan en las computadoras, debido a que éstas trabajan internamente con dos niveles de voltaje, por lo cual su sistema de numeración natural es el sistema binario (encendido 1, apagado 0).

sistema octal

El sistema numérico en base 8 se llama octal y utiliza los dígitos del 0 al 7.

En informática a veces se utiliza la numeración octal en vez de la hexadecimal. Tiene la ventaja de que no requiere utilizar otros símbolos diferentes de los dígitos. Sin embargo, para trabajar con bytes o conjuntos de ellos, asumiendo que un byte es una palabra de 8 bits, suele ser más cómodo el sistema hexadecimal, por cuanto todo byte así definido es completamente representable por dos dígitos hexadecimales.

El sistema de numeración octal es un sistema de numeración en base 8, una base que es potencia exacta de 2 o de la numeración binaria. Esta característica hace que la conversión a binario o viceversa sea bastante simple. El sistema octal usa 8 dígitos (0, 1, 2, 3, 4, 5, 6, 7) y tienen el mismo valor que en el sistema de numeración decimal.

sistema hexadecimal

sistema hexadecimal es el sistema de numeración posicional que tiene como base el 16. Su uso actual está muy vinculado a la informática y ciencias de la computación, pues los computadores suelen utilizar el byte u octeto como unidad básica de memoria; y, debido a que un byte representa

2^8

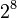valores posibles, y esto puede representarse como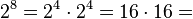

2^8 = 2^4 \cdot 2^4 = 16 \cdot 16 =

1 \cdot 16^2 + 0 \cdot 16^1 + 0 \cdot 16^0

, que equivale al número en base 16

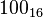100_{16}

, dos dígitos hexadecimales corresponden exactamente a un byte.

En principio, dado que el sistema usual de numeración es de base decimal y, por ello, sólo se dispone de diez dígitos, se adoptó la convención de usar las seis primeras letras del alfabeto latino para suplir los dígitos que nos faltan. El conjunto de símbolos sería, por tanto, el siguiente:

$S = \{0, 1, 2, 3, 4, 5, 6, 7, 8, 9, \mathrm{A}, \mathrm{B}, \mathrm{C}, \mathrm{D}, \mathrm{E}, \mathrm{F}\}\,$

Hexadecimal Decimal

A 10

B 11

C 12

D 13

E 14

F 15

Hexadecimal	Decimal
A	10
B	11
C	12
D	13
E	14
F	15

Mi perfil

sebastian fernandez martinez

"¿Mi más grande motivación? Seguir retándome a mí mismo. Veo la vida como una larga educación universitaria"

soy emprendedor con los objetivos propuestos

trabajo en una compañía dedicada básicamente a el ensamble de carro-serias de diferente tipo de chasis.

Marco polo es una empresa con más de 50 años de tradición

en el país, se ha destacado por ser líder en el segmento de carrocerías para buses.